
Här får du lära dig mer om kartprojektionens grunder och olika typer av kartprojektioner.
När man avbildar den krökta jordytan – eller egentligen jordmodellen, som är en ellipsoid eller sfär – på ett plan, kan det inte ske utan formförändring. Med en lämpligt vald projektion kan man däremot hålla formförändringarna inom vissa gränser, inom det geografiska område man arbetar med.
Jordmodellen
För mycket småskaliga kartor, till exempel världskartor, använder man en sfärisk jordmodell, på grund av att det ger enklare beräkningar. Då får man en avbildning som inte blir lika noggrann som om man använt ellipsoidisk jordmodell. Eftersom felen är ganska små och noggrannheten ändå inte är särskilt hög i världskartor kan felen försummas.
För storskalig kartläggning, till exempel topografiska kartor, används alltid en ellipsoidisk jordmodell. Den liknar jordens faktiska form bättre, med avplattning vid polerna. Det leder till krångligare formler, där man måste använda matematiska serieutvecklingar.
Även i karttjänster för mobila plattformar, som till exempel mobiltelefoner, används ofta en sfärisk jordmodell. Projektionen som används kallas ofta Web Mercator. Kartan i telefonen kan vara mindre noggrann men eftersom din position också visas med samma kartprojektion så märker du det inte.
Kartprojektionens konstruktion
Metoden för att konstruera kartprojektionen kan delas in i tre huvudtyper vad gäller
- formen på projektionsytan: cylindrisk, konisk eller azimutal
- placeringen av projektionsytan: normal, transversal eller snedaxlig.
Längre ner på sidan hittar du ett exempel som stegvis visar hur en kartprojektion går till. Exemplet visar en transversal cylindrisk projektion, en så kallad Transversal Mercator- eller Gauss-Krügers projektion, som är den vanligaste kartprojektionen i Sverige. Du kan applicera exemplet på de andra typerna av projektioner.
Cylindrisk projektion
Man använder en cylinder som tangerar ekvatorn (man får då en projektion av normal typ; bilden till vänster), eller längs en medelmeridian (projektionen är då av transversal typ; bilden till höger):
Dessutom kan man använda en snedaxlig typ med annan orientering av cylindern.
Konisk projektion
Om du använder en konisk projektion tangeras jordklotet av en kon. Vanligtvis tangerar konen jordklotet längs en parallellcirkel. Projektionen sägs då vara av normal typ:
Azimutal projektion
Azimutal kartprojektion använder ett plan som tangerar jordklotet i en punkt. Normal typ, när tangeringspunkten är en av polerna, kallas oftast polär aspekt. Transversal typ, om tangeringspunkten ligger på ekvatorn, kallas oftast ekvatoriell aspekt. Även snedaxlig typ används. I bilden nedan kan du se polär aspekt:
Perspektivisk avbildning
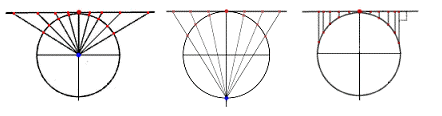
En perspektivisk projektion kan konstrueras rent geometriskt. Låt räta linjer, projektionsstrålar, utgå från en punkt, projektionscentrum. De punkter på klotytan som avbildas, förlängs av projektionsstrålarna tills de skär projektionsytan i punkternas avbild. Som exempel har vi den gnomoniska projektionen (bild nedan till vänster). Den är en azimutal projektion där projektionscentrum är jordklotets medelpunkt. Stereografisk projektion (bild nedan i mitten) där projektionscentrum är tangeringspunktens antipod. Ortografisk projektion (bild nedan till höger) där projektionscentrum är placerat på oändligt avstånd. Det gör att projektionsstrålarna är parallella. Projektionerna visas i nordpolsaspekt.
Avbildningsfunktion
De flesta projektioner som vi använder är inte perspektiviska. Avbildningen sker på ett mer komplicerat sätt och kan beskrivas allmänt som en matematisk funktion:
x = fx(j, l)
y = fy(j, l)
där j är geodetisk latitud, l är geodetisk longitud och x, y är plana koordinater i projektionsplanet.
I Sverige och en del andra länder är konventionen att x-axeln i detta sammanhang är riktad mot norr och y-axeln mot öster, med positiv omloppsriktning medsols, alltså omvänt mot skolboksgeometrin, där y-axeln är riktad uppåt och x-axeln åt höger, med positiv omloppsriktning motsols. För att undvika förväxling kallas ibland axlarna 'Northing' respektive 'Easting', vilket vi också har börjat använda i Sverige för de olika projektionerna av SWEREF 99, fortfarande med positiv omloppsriktning medsols.
Viktiga egenskaper
Genom att formulera villkor för avbildningsfunktionen kan man ge projektionen olika egenskaper. De viktigaste egenskaperna är konformitet (eller vinkelriktighet), ytriktighet och längdriktighet.
Konformitet
Vinkelriktig, eller formbevarande, projektion innebär att om en oändligt liten figur projiceras, avbildas den utan formförändring. Förstoringen i en punkt är lika stor i alla riktningar. Man kan inte kombinera vinkelriktighet med ytriktighet.
I geodetiska sammanhang används normalt konforma (vinkelriktiga) projektioner, alltid från en ellipsoidisk jordmodell. En egenskap som är av särskilt intresse hos konforma projektioner är meridiankonvergensen.
Ytriktighet
Ytan hos en figur på klotytan avbildas i kartplanet på en figur med lika stor yta. Ytriktighet kan inte kombineras med vinkelriktighet.
Längdriktighet
Denna egenskap kan inte gälla allmänt, utan endast längs vissa linjer, till exempel längs medelmeridianen eller en parallellcirkel.
Tissots indikatris
Med den så kallade indikatrisen, eller Tissots indikatris, kan man avläsa egenskaperna för en projektion. Tissots indikatris är den ellips som uppkommer vid projektionens avbildning av en elementarcirkel på klotytan. (En elementarcirkel är en oändligt liten cirkel.)
Vid normala projektioner blir indikatrisens axlar förlagda längs meridianen och parallellen genom den avbildade punkten. Om elementarcirkelns radie väljs lika med ett (1), så blir förstoringarna h och k utefter meridian och parallell, i det normala fallet, lika med halvaxlarnas längder i indikatrisen.
Ur indikatrisens egenskaper kan olika typer av projektioner identifieras:
- Om h = k är projektionen konform (vinkelriktig).
- Om h * k = 1 är projektionen ytriktig.
- Om h = 1 (k = 1) är projektionen längdriktig utefter meridianen (parallellen).
Indikatrisen ger också information om projektionens vinkelförvridning i punkten. Maximala beloppet w fås ur formeln:
sin (w) = | (k - h) / (k + h) |
Projektionsparametrar
Vid specifikation av en projektion behöver du ange, förutom den allmänna typen, till exempel Gauss-Krüger, ett antal parametrar.
Jordellipsoidens parametrar måste du alltid ange, men de ges ofta indirekt av det geodetiska datum eller referenssystem som används.
De övriga parametrar som brukar förekomma är:
- Medelmeridian (engelska: central meridian); mittmeridian som normalt avbildas som en vertikal rät linje och utgör symmetriaxel, och det plana systemets naturliga x-axel. Longituden (grader, minuter, sekunder) för medelmeridianen anges, vanligen relativt internationella nollmeridianen i Greenwich.
- Standardparalleller (engelska: standard parallel); anges för normala projektioner, och är parallellcirklar som avbildas skalenligt. En projektion kan ha en eller två standardparalleller. Latituden för dessa anges.
- Skalreduktionsfaktor (engelska: scale factor eller scale on central meridian); ett tal, mindre än eller lika med 1, som appliceras på koordinaterna för att omfördela skalfelet i projektionen. Till exempel i UTM används skalreduktionsfaktorn 0,9996.
- Tangeringspunktens latitud; centrumpunkt för azimutala projektioner. Latituden anges.
Ett antal parametrar används för att mer eller mindre godtyckligt omdefiniera projektionssystemets origo:
- x0 (engelska: false northing), x-tillägg (även negativa värden, för avdrag)
- y0 (engelska false easting), y-tillägg (även negativa värden, för avdrag)
De följande används normalt inte i Sverige:
- Latitud för origo (engelska: latitude of origin); här anges att det plana systemets origo ska förläggas på en viss latitud.
- Longitud för origo (engelska: longitude of origin); här anges att det plana systemets origo ska förläggas på en viss longitud. Är normalt detsamma som medelmeridianens longitud.
Exempel på konstruktion av en kartprojektion
Följande exempel visar stegvis hur du kan avbilda en punkt som har geodetiska koordinater (latitud, longitud) på en plan yta, till exempel en karta. Du kan också följa exemplet baklänges, det vill säga om din punkt har plana koordinater och du vill omvandla dem till geodetiska koordinater. Exemplet visar Transversal Mercator som är vanligast i Sverige men det går bra att byta ut cylindern mot en annan geometrisk figur, till exempel en kon.
1. Du har en punkt (röd i figuren) med de geodetiska koordinaterna (latitud=j, longitud=l).
2. Nu placerar du en liggande cylinder som tangerar jorden vid den valda medelmeridianen (orange i figuren). Genom att avbilda den röda punkten på cylindern får du den gröna punkten.
3. I detta steg vecklar du ut cylindern till en plan yta.
4. Nu är du klar. Din ursprungliga punkt är nu uttryckt i ett plant koordinatsystem, som en grön punkt i figuren.

